
Reasons of Underdevelopment – Todaro & Smith
• 낮은 수준의 생활 및 생산성
• 낮은 수준의 인적 자본
• 높은 수준의 불평등과 절대 빈곤
• 높은 인구 증가율
• 사회적 분절화 확대 (Greater social fractionalization)
• 많은 농촌인구 및 도심으로의 급속한 이주
• 낮은 수준의 산업화
• 역지리 (Adversegeography)
• 저개발 금융 및 기타 시장
• 열악한 제도 및 종종 외부 의존성과 같은 식민지의 지속적인 영향(Lingering colonial impact)
<생산성의 결정 변수>
* 생산요소 : 재화와 서비스의 생산에 사용되는 투입요소(factors of production)
- 물적자본 (Physical Capital) : 설비, 장비, 건물
- 인적자본 (Human Capital) : 교육, 훈련
- 자연자원 (Natural Resources) : 반드시 도움이 될까?
- 기술지식 (Technological Knowledge)
: 자본(capital)은 만들어진 생산요소임. 즉 자본이라는 생산요소는 과거 생산활동의 산출물임
: 생산요소가 생산성을 결정함
* 물적자본 : 인당 물적자본은 재화와 서비스 생산에 사용될 수 있는 장비와 건물의 재고를 말함
- 물적자본의 예
: 건축이나 자동차 수리에 사용되는 연장
: 가구 제조에 사용되는 연장
: 오피스 건물, 학교 건물 등
물적자본은 생산된 요소임
물적자본은 과거 생산과정을 통해 생산된 산출물로서 생산에 투입되는 요소임
* 인적자본 : Human capital 근로자 1인당 인적자본은 교육, 훈련, 경험을 통해 근로자들이 체득한 지식과 기술을 말함 / 물적자본과 마찬가지로 인적자본도 한 나라경제의 생산능력을 제고함
* 자연자원 : 자연자원은 토지, 강물, 광물 등처럼 자연에 의해 제공되는 생산요소임
- 회복 가능한 자원 (Renewable resources) : 목재와 임야
- 회복 불가능 자원 (Nonrenewable resources) : 석유와 석탄 자연자원은 한 경제의 생산능력을 높이는데 중요하지만 꼭 필요한 것은 아님
* 기술지식 : 기술지식(Technological knowledge)은 재화와 서비스를 생산하는 최선의 방법에 대한 사회의 이해를 나타냄 / 인적자본에는 이러한 기술지식을 노동력에 전파하는데 소요되는 자원이 포함됨
<생산함수>
Y = A F(L, K, H, N)
Y = 산출량
A = 생산기술
L = 노동의 투입량
K = 물적자본의 투입량
H = 인적자본의 투입량
N = 자연자원의 투입량
F= Production Function
생산함수 F( ) = 생산함수 : 생산요소 투입량과 산출량 사이의 관계
규모에 대한 보수 불변과 생산성
규모에 대한 보수불변의 경제에서 생산성(Y/L = 근로자 1인당 산출량)의 결정요인
Y / L = A F (1, K/L, H/L, N/L )
•Y/L = 근로자 1인당 산출량
•K/L = 근로자 1인당 물적자본
•H/L =근로자 1인당 인적자본
•N/L = 1인당 자연자원
생산성 (Y/L)의 결정요인
- K/L = 근로자 1인당 물적자본
- H/L =근로자 1인당 인적자본
- N/L = 1인당 자연자원
- 기술조건 (A)
규모에 대한 보수불변 : 모든 생산요소의 투입량이 2배로 늘면 산출량도 2배 증가
<경제성장을 촉진하는 정부정책>
- 저축과 투자의 장려
- 교육과 훈련의 장려
- 정치적 안정과 재산권의 확립
- 자유무역의 촉진(대한민국 / 북한)
- 외국자본의 유치
- 연구개발의 장려(민간 / 공공, 특허)
[경제학] 생산성과 성장율 그리고 GDP
생산성은 GDP를 결정하고, GDP는 삶의 질을 결정한다 2004-1-5 잘사는 나라와 못사는 나라, 그리고 부자와 가난한 사람. 한 개인이나 한 국가나 부유한 측이 있고 그렇지 못한 측이 있습니다. 무엇이
ltvw.tistory.com
생산함수
위에서 살펴 본 생산성 결정 요인들이 모두 조화가 되어서 최종적으로 한 국가의 생산량, 즉 GDP를 결정합니다. 이것을 식으로 써보면,
Y = A F(L,K,H,N) 입니다.
Y는 생산량
A는 생산기술
L은 노동량
H는 인적자본의 크기
K는 자본(재)의 크기
N은 자연자원의 크기입니다.
위 식을 생산함수라 하며 이 때 산출량 Y와 투입요소 L,K,H,N 사이에는 수확불변(Constant returns to scale)의 관계가 있습니다. 그래서 L,K,H,N을 2배 늘리면 Y도 2배가 늘어납니다.
xY = A F(xL,xK,xH,xN)
또는 생산기술 A가 뛰어난 경우도 (=변수 A값이 커지는 경우) Y가 커집니다.
따라서 L,K,H,N을 늘리거나 A값을 늘려야 국부가 증가합니다.
A값이 작다면, 즉, 다른 나라에 비해 생산기술이 떨어지면 더 많은 노동시간과 더 많은 자본재와 더 많은 인적자본과 더 많은 자연자원을 사용해야 동일한 Y를 기록할 수 있습니다.
최근 많이 얘기되고 있는 중국의 경우를 생각해 봅시다. 중국은 세계 최고 수준의 노동량(노동력)과 자본재(중국이 유치하는 외국 자본이 투자를 해서 구축한 자본재는 모두 중국의 생산량을 늘려주는 데 활용됩니다), 뛰어난 인적자원(미국 유학파의 상당수가 중국계이며, 이들은 귀국해서 국가 발전을 위해 기여하겠다는 얘기들을 많이 하고 있습니다.), 그리고 자연자원을 보유하고 있습니다.
약간 부족한 것은 그야말로 생산기술 하나뿐인데, 이마저 최근 급속도로 발전하고 있습니다. 따라서, 조만간에 중국은 세계 최고 수준의 Y를 갖게 됩니다.
그리고 그들이 갖고 있는 그 방대한 시장은 더 많은 K를 끌어들일 것이며, 그에따라 더 많은 H도 끌어들이게 될 것입니다. 우리나라가 과연 어떻게 해나가야 할 지 위기감이 들지 않을 수 없습니다.
<경제성장론의 발전>
• 아담 스미스: 경제성장의 동인으로서 분업 Y=F(D), D:분업 분업은 숙련도를 향상, 공정간의 이동 비용을 절감, 기계발명 촉진, 즉, 분업은 H, K, A에 영향을 미친다고 주장.
• 맬더스: 산출량은 노동의 함수 Y=F(L), L:노동인구 그러나 노동인구에는 수확체감의 법칙 적용, 따라서 인간은 빈곤에서 벗어날 수 없음.
• 솔로우의 근대경제성장론 Y=F(L, K), 기술발전은 산출량에서 L과 K의 기여분을 제외한 잔차로서 정의
• 내생적 경제성장론(endogenous growth theory) Y=AF(H, K) H혹은 K의 증가는 외부성을 가져서 A를 증가시킴.
콥-더글러스 생산함수
콥-더글라스 생산 함수(Cobb–Douglas production function)는 한계생산력과 임금 사이의 관계를 규명하기 위해 창안된, 대표적인 1차 동차 생산함수이다.
- Y는 생산량(Q)으로 대체할 수 있다.
- A와
는 생산기술에 의하여 결정되는 상수이다.
- L은 노동투입량이다.
- K는 자본투입량이다.
만약 노동과 자본의 투입량을 k배 만큼 증가시켰을 경우 생산량은
일 경우 k배 이상으로 증가하여 규모의 경제가 발생하고,
인 경우 k배 만큼 증가하여 규모가 변화하여도 수익은 변하지 않으며
인 경우 k배보다 적게 증가하여 규모의 불경제, 즉 규모에 따른 수익 체감이 발생한다.

GDP: 중요하고 다양한 개념들
– GDP = 총소득 = 총산출 = 총지출 = 최종재의 각 생산단계에 서의 부가가치의 합계
– 총산출 :기술(노동+자본) ⇒ Y=F(K,L) p
– 총소득 :(노동소득+자본소득) ⇒ Y=(MPKⅹK)+(MPLⅹL)
– 총지출 :[소비+투자+정부지출+(수출-수입)] ⇒ Y=C+I+G+NX
※ 타국과 무역을 하지 않는 폐쇄경제 가정(NX=X-M=0)
– 총저축 :(민간저축+정부저축) = (Y-T-C)+(T-G) = Y-C-G = I
※ 소비 = 기초소비 + 가처분소득 비례 소비[MPCⅹ(Y-T)] p69
생산요소(Factors of production)
K = 자본(capital): 노동자가 사용하는 일련의 수단 생산에 사용되는 도구, 기계, 및 장비
L = 노동(labor): 일하는데 사용한 시간 노동자들의 물적 및 정신적 노력
생산함수
• 함수형태 Y = F(K, L)
• 한 경제가 K 단위의 자본과 L 단위의 노동을 결합하여 얼마나 많은 생산(Y )을 할 수 있는 지를 보여준다.
• 한 경제의 기술수준을 반영하고 있다.
• 규모에 대한 보수불변(constant returns to scale)의 속성을 나타내 고 있음 : 자본 및 노동이 10% 증가하면 생산량도 10% 증가
처음에는 Y1 = F (K1 , L1 )이라고 가정하자.
모든 투입물을 z배만큼 증가시키면:
K2 = zK1 and L2 = zL1
(예를 들어, z = 1.25라면, 모든 투입물은 25% 증가한 것이다)
이 때 생산 Y2 = F (K2 , L2 )은 얼마나 증가할까?
• 규모에 대한 보수불변 (constant returns)이면 Y2 = zY1
• 규모에 대한 보수증가 (increasing returns)이면 Y2 > zY1
• 규모에 대한 보수감소 (decreasing returns)이면 Y2 < zY1
1. 기술수준은 고정되어 있다.
2. 한 경제의 자본과 노동의 공급은 고정되어 있다.

<GDP의 결정>
생산량은 고정된 생산요소의 공급과 기술수준에 의하여 결정된다:

<국민소득의 분배>
• 기업이 생산요소에 대하여 지불하는 단위 당 가격인 요소가격 (factor prices)에 의하여 결정된다.
– 임금(wage) = 노동(L)의 가격
– 임대료(rental rate) = 자본(K)의 가격
W = 명목임금(nominal wage)
R = 명목임대율(nominal rental rate)
P = 생산물의 가격(price of output)
W /P = 생산물의 크기로 측정된 실질임금(real wage)
R /P = 실질임대율(real rental rate)
노동에 대한 수요(Demand for labor)
• 노동시장은 경쟁적이라고 가정한다: 각 기업은 W, R, 및 P를 주어진 것을 받아들인다.
• 기초적 아이디어: 기업은 비용이 수익을 초과하지 않는 한 노동을 더 고용한다.
– 비용(cost) = 실질임금(real wage)
– 편익(benefit) = 노동의 한계생산물(marginal product of labor)
<노동의 한계생산물 (MPL)과 생산함수>

한계수확의 체감 (Diminishing marginal returns)
• (다른 것은 일정할 때) 요소의 투입량이 증가함에 따라, 한계생산물 은 감소한다.
• 직관적 해석: K는 고정되어 있고 L을 증가시키는 경우를 생각해보자.
노동 한 단위당 기계의 숫자는 줄어든다(주방이 더 혼잡).
따라서 노동생산성은 하락한다.
분배에 관한 신고전학파 이론 (The Neoclassical Theory of Distribution)
• 각 요소 투입물은 그 요소의 한계생산물 만큼 보수를 받는다.
• 대부분의 경제학자들에 의하여 수용되고 있다.

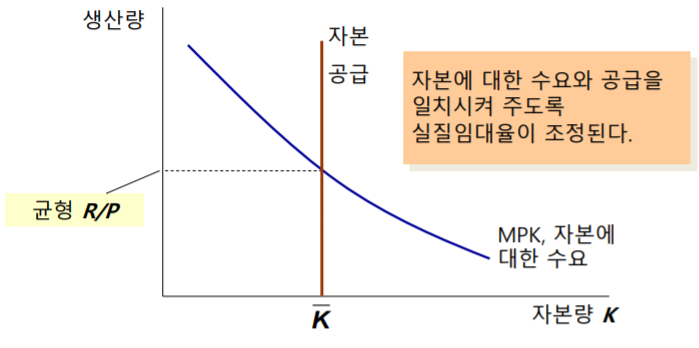
MPL과 노동에 대한 수요 (Demand for labor)

균형임대율 (The equilibrium real rental rate)

*****************
• 콥-더글라스 생산함수에서의 요소소득 분배율은 일정하다:
a = 총소득에 대한 자본소득 분배율:
자본소득 = MPK x K = a Y
노동소득 = MPL x L = (1 – a )Y

• 코브-더글라스 생산함수의 형태: 여기서 A는 기술수준을 나타낸다
• 각 요소의 한계생산물은 평균생산물에 비례한다:
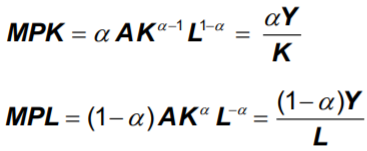
이윤 = 수입 - 노동비용 - 자본비용
= PY - WL - RK
= PF(L, K) - WL - RK
이윤은 생산물가격(P), 요소가격(W, R), 요소량 L, K 에 의존한다. 경쟁상태 하의 기업은 생산물가격과 요소가격을 주어진 것으로 간주하고 이윤을 극대화시키는 노동과 자본량을 선택한다.
기업이 고용규모를 확대하면 할수록 생산량은 증대한다. 노동의 한계생산물(marginal product of labor, MPL)은 자본량은 일정하다고 보고 기업이 노동을 한 단위 더 투입시킴으로써 얻게 되는 생산량의 증가분을 의미한다. 대부분의 생산함수들은 자본량이 고정된 경우 노동량이 증대됨에 따라 노동의 한계생산물이 감소하는 한계생산물 체감의 속성을 갖고 있다.
경쟁상태 하에서 이윤극대화를 추구하는 기업이 노동 고용규모의 증대여부를 결정하려는 경우 기업은 이런 결정이 이윤에 미치는 효과를 고려할 것이다.
따라서 고용규모를 증가시킬 경우 얻는 생산규모의 증대로 인한 수입증대와 임금지불에 따른 비용증대를 비교하게 된다. 고용증가로 인한 수입의 증대는 노동의 한계생산물과 생산물 가격에 의존한다.
△이윤 = △수입 - △비용
= (P × MPL) - W
기업은 얼마만큼의 노동을 고용할 것인가? 기업경영인은 증대된 수입 (P × MPL)이 임금 W를 초과하면 노동의 고용증가로 이윤이 증대될 것이라는 점을 깨닫게 된다.
따라서 기업인은 추가적으로 고용된 노동이 이윤을 발생시키지 않을 때까지, 즉 증대된 수입과 임금이 같아지는 점으로 MPL이 하락할 때까지 노동 고용규모를 증가시킬 것이다. 기업의 노동수요는
P × MPL = W
MPL = W/P
여기서 W/P는 화폐가치보다 생산량 단위로 측정한 노동에 대한 보수인 실질임금이다. 이윤을 극대화하기 위하여 기업은 노동의 한계생산물이 실질임금과 같아지는 점까지 고용하게 된다.
자본의 한계생산물(marginal product of capital, MPK)은 노동량은 일정하다고 보고 기업이 자본을 한 단위 더 투입시킴으로써 얻게 되는 생산량의 증가분을 의미한다.
기계 한 단위를 더 임대하여 얻은 이윤의 증가는 그 기계 투입으로 생산된 생산량을 판매하여 취득한 수입 증대분에서 기계의 임대가격을 감하여 얻을 수 있다.
△이윤 = △수입 - △비용
= (P × MPK) - R
이윤극대화를 위해 기업은 MPK가 하락하여 실질 임대가격과 같아질 때까지 계속 자본을 임대하게 된다.
MPK = R/P
경쟁상태 하에서 이윤극대화를 추구하는 기업은 노동의 고용규모와 자본의 임대규모를 단순한 규칙에 따라 결정한다. 즉, 요소의 한계생산물이 감소하여 실질요소가격과 같아질 때까지 기업은 각각의 생산요소를 수요한다.
마. 국민소득의 분배
경제의 모든 기업들이 경쟁상태에 있고 이윤극대화를 추구할 경우 각 생산요소는 생산과정에 투입된 한계생산물에 해당하는 대가를 지급받게 된다. 기업이 각 생산요소들에게 지불한 후 남는 소득은 기업 소유주의 경제적 이윤(economic profit)이 된다.
경제적 이윤 = Y - (MPL×L) - (MPK×K)
Y = (MPL×L) +(MPK×K) + 경제적 이윤
총소득은 노동에 대한 보상, 자본에 대한 보상, 경제적 이윤 등으로 분배된다. 생산함수가 규모에 대해 수확불변의 속성을 갖는 경우 경제적 이윤은 ‘0’이 되어야 한다(오일러의 정리). 즉,
F(K, L) = (MPL×L) +(MPK×K)
각 생산요소가 한계생산물에 따라 대가를 받는다면 이런 요소 지급의 합계가 총생산량이 된다.
즉 규모에 대한 수확불변, 이윤극대화, 경쟁 모두가 경제적 이윤이 ‘0’이 된다는 것을 의미한다.
총생산량은 자본과 노동에 각각의 한계생산성에 따라 분배된다.
솔로우 모형
위키백과, 우리 모두의 백과사전.
솔로우 모형(Solow model)은 장기 경제 성장을 설명하는 경제 모형이다. 1956년에 로버트 솔로우가 고안한 모형[1]으로 신고전학파 생산함수를 기반으로 외생적 인구 증가, 외생적 기술 진보를 가정하였다. 이 모형을 고안한 로버트 솔로우는 1987년 경제 성장 이론에 대한 기여로 노벨 경제학상을 수상하였다.[2]
솔로우 모형은 자본과 노동이 고정비율로 결합하는 것을 가정하는 해로드-도마 모형과는 달리 자본과 노동 사이의 대체가 가능한 생산함수를 가정한다. 생산함수는 한계생산성이 체감하고, 규모에 대한 수익 불변의 특성을 갖는다.
생산함수는 다음과 같이 주어진다. 균형 성장 경로를 갖는 생산함수는 반드시 노동증대형 생산함수(labor-augmenting production function)여야 하므로,[3] 노동증대형 생산함수를 가정한다. 여기서
는 GDP를,
는 자본을,
는 기술 수준을,
은 노동을 의미하며, 기술 수준과 노동량을 곱한
은 유효 노동이다.
기술 진보율과 노동 증가율은 다음과 같이 외생적으로 결정된다고 가정한다.
생산함수는 규모에 대한 수익 불변이므로, 위의 생산함수의 양변을 유효 노동으로 나누어, 생산함수를 유효 노동당 자본에 관한 1변수함수로 간단히 표현할 수 있다.
는 유효 노동당 산출량을,
는 유효 노동당 자본을 의미한다.
한편, 자본축적은 신규투자에서 감가상각을 뺀 것이다. 폐쇄 경제에서 투자는 저축과 같으며, 저축률
와 감가상각률
는 외생적으로 결정된다고 가정한다. 자본축적 방정식은 다음과 같다.
유효노동 1단위당 자본축적 방정식은 다음과 같이 표현할 수 있다.[note 1]
유효 노동 1단위당 자본은
이 되는 균제 상태(steady state)으로 접근하게 된다. 저축률이 높아질 경우에는 균제 상태가 되는 유효 노동 1단위당 자본이 보다 높은 수준에서 결정될 것이다.
그러나 저축률이 높아진다 하더라도 새로운 균제 상태로 이동하는 동안에만 성장률이 높아지는 효과가 발생할 뿐이므로 저축률의 상승이 장기적인 경제 성장을 유발시키지는 않는다.
요컨대, 저축률의 증가는 균제 상태가 되는 유효 노동 1단위당 자본량이 높아지는 수준 효과(level effect)만을 일으킬 뿐 장기적인 성장 효과를 일으키지 못한다.

균형 성장
자본, 노동, 생산량이 일정한 비율로 성장하는 경로를 균형성장경로(balanced growth path, BGP)라고 한다.[5] 솔로우 모형에서 유효 노동 1단위당 자본이 균제 상태에 도달하면 균형성장경로를 따르게 된다. 균형성장경로에서 산출량-자본 비율은 일정하며, 1인당 산출량과 1인당 자본의 성장률은 기술진보율과 같다.
균형성장경로에서 자본의 실질임대료는 시간이 지나도 일정하며, 실질임금은 기술진보율과 같은 비율로 성장한다.
[경제성장이론 ①] 솔로우 모형 - 자본축적을 통한 경제성장
※ 왜 어떤 나라는 잘 살고, 또 어떤 나라는 못 사는 것일까? 지속적인 경제성장을 위한 동력은 무엇일까? 경제성장은 생활수준을 대폭 향상시켜 줍니다. 너무나 당연해 보이는 이 명제는 대
joohyeon.com
"왜 어떤 나라는 잘 살고, 또 어떤 나라는 못 사는 것일까요?"(why are we so rich and they so poor?).
"지속적인 경제성장을 위한 동력은 무엇일까?"(engine of growth)
2가지 질문에 대한 해답을 얻기 위해서 가장 먼저 살펴봐야 할 경제성장 이론은 바로 '솔로우 모형'(Solow Growth Model) 혹은 '신고전파 모형'(Neoclassical Growth Model) 입니다. 명칭에서 알 수 있듯이, 이 모형은 경제학자 로버트 솔로우(Robert Solow, 1987년 노벨경제학상 수상)가 제시했습니다.
그는 1956년 논문 <경제성장 이론에 대한 기여>(<A Contribution to the Theory of Economic Growth>) 를 통해, 미국이 겪어온 경제성장 과정을 이론화 하였습니다.
미국의 성공경험이 알려준 것은 '자본축적의 중요성'(Capital Accumulation) 이었습니다. 미국의 1인당 자본량은 꾸준하게 증가해왔으며, 이에 맞추어 1인당 생산량도 늘어났습니다.
따라서, 솔로우는 "경제성장을 달성하려면 자본축적이 필요하다"고 주장합니다.
이제부터 솔로우 모형을 자세히 살펴보면서 경제성장을 달성하고 유지하기 위해 필요한 것을 알아봅시다.
한 국가가 경제성장을 이루었는지 여부는 '1인당 생산량'(per capita GDP)으로 파악할 수 있습니다. 현대 자본주의에서 중요한 것은 '생산'1이기 때문이죠.

출처 : OECD National Accounts at a Glance
윗 그래프는 미국의 1인당 생산량 및 자본량 추이를 보여주고 있습니다. 앞서 말했듯이, 미국의 1인당 생산량은 계속해서 늘어났고, 그 배경에는 1인당 자본량 증가가 있습니다.
여기서 말하는 자본이란 '물적자본'(physical capital)을 의미합니다. 공장설비 및 기계 등이 더 많이 도입될수록 생산량도 비례하여 증가하게 됩니다.
이를 보면, 1인당 생산량 증가, 다시 말해 경제성장을 달성하기 위해 필요한 것은 '(물적)자본축적'(Capital Accumulation) 이라는 걸 직관적으로 깨달을 수 있습니다. 솔로우 모형은 '자본을 축적하는 과정 및 축적된 자본이 생산량 증가로 이어지는 과정'을 아주 쉽게 설명해주고 있습니다.

윗 수식은 저축과 투자가 1인당 자본량을 늘리는 과정을 보여주고 있습니다. 이른바 '솔로우 모형의 기본 방정식'(Fundamental Equation of the Solow Model) 입니다.
경제원론을 소개한 '[경제학원론 거시편 ⑤] 한정된 자원을 효율적으로 사용하여 경제성장 달성하기 - 저축과 투자'2 에서 보았듯이, 자본축적을 위해 필요한 것은 '투자'(investment)와 '저축'(saving) 입니다.
투자란 '기계 · 생산설비 등 신규 자본재를 만들거나 구매하는 것'을 뜻하며, 저축은 '생필품 소비를 덜하여서, 자본재 생산에 더 많은 자원을 배치하는 것'을 의미합니다. 한 국가의 저축이 많을수록 투자도 비례적으로 증가하여 자본축적이 이루어지게 됩니다.
1인당 생산량 중 일정부분을 소비하지 않고 저축하면 투자로 이어지고 이는 곧 1인당 자본량 증가로 나타납니다. 증가된 자본량은 1인당 생산량을 늘리게 되고, 늘어난 생산량 중 일정부분을 또다시 저축 · 투자로 연결시키면 자본량과 생산량이 더욱 늘어나는 선순환이 발생하게 됩니다.
이때 1인당 자본량이 계속해서 늘어나는 건 아닙니다. 기계 · 생산설비 등 자본량은 감가상각의 영향을 받아 일정량 사라집니다. 또한, 인구가 많아질수록 '1인당'(per capita) 자본량도 줄어들기 때문에, 인구증가율에 비례하여 소모됩니다.
따라서, 1인당 자본량은 '저축' 및 '투자'가 증가할수록 늘어나며, '감가상각률' 및 '인구증가율'이 높아질수록 줄어듭니다.
(사족 : 경제 전체 '총'자본량을 기준으로 생각하면, 인구가 많아질수록 '총'자본량은 증가하고, '총'생산량 또한 늘어납니다. '1인당' 자본량 및 생산량이 늘어나는 것을 '자본심화'(Capital Deepening) 라하고, '총' 자본량 및 생산량이 증가하는 것을 '자본확장'(Capital Widening) 이라 합니다.)
이러한 논리로부터, 우리는 "왜 어떤 나라는 잘 살고, 또 어떤 나라는 못 사는 것일까요?"(why are we so rich and they so poor?)에 대한 해답을 얻을 수 있습니다.
|
▶ 어떤 국가가 잘 사는 이유는 높은 저축율 · 낮은 인구증가율 등에 힘입어 1인당 자본을 많이 축적했기 때문입니다.
▶ 또 어떤 국가가 못 사는 이유는 낮은 저축율 · 높은 인구증가율 때문에 1인당 자본을 적게 축적했기 때문입니다.
|
한 국가가 생필품 소비를 많이 하여서 자본재 생산에 더 적은 힘이 배분된다면(=소비가 많아 저축과 투자가 적다면), 그 국가는 자본축적이 더뎌져서 생산량도 크게 늘어나지 않습니다. 또한, 경제성장 초기 높은 인구증가율은 자원을 (생산에 참여하지 않는) 유아에게 배분케하여 (생산에 참여하는) 성인의 1인당 자본량을 훼손시킵니다.
경제성장을 도모하려는 국가가 초기에 '저축증대'와 '산아제한'을 실시하는 이유가 바로 여기에 있습니다. 과거 한국도 마찬가지로 저축장려 및 강력한 산아제한 정책을 실시했었죠.
※ 자본축적 만으로 지속적인 성장이 가능할까?
- 자본량 증가에 대한 생산량 증가폭은 체감
- 영구적인 성장을 위해 필요한 것은 '기술진보'
지금까지 논의한 것은 '1인당 생산량 수준'(per capita GDP Level)에 관한 것이었습니다. 저축율이 높고 인구증가율이 낮을수록, 자본축적이 일어나 생활'수준'이 높아지게 됩니다.
그렇다면 생활'수준' 향상은 얼마나 빨리 달성가능하며 언제까지 지속되는 것일까요?
경제성장 달성에 중요한 것은 성공여부 뿐 아니라 성공에 걸리기까지의 시간 및 지속적인 성장 여부도 있습니다. 자본축적을 통해 생활수준이 향상되더라도, 그것이 엄청 오래 걸려서 내가 죽기 전에 이루어지지 않으면 아무런 의미가 없습니다. 또한, 한번 생활수준이 향상된 후 지속되지 않는 것도 의미가 없습니다.
이를 파악하기 위해 구분해야 할 개념은 '수준'(level)과 '성장'(growth) 입니다.
어떤 나라가 잘 사느냐 못 사느냐 따지는 것은 '수준'(level)을 이야기 하는 것입니다. 반면, 어떤 나라가 얼마나 빨리 생산량을 늘리느냐, 지속적인 성장세를 유지하느냐는 '성장'(growth)을 의미합니다.
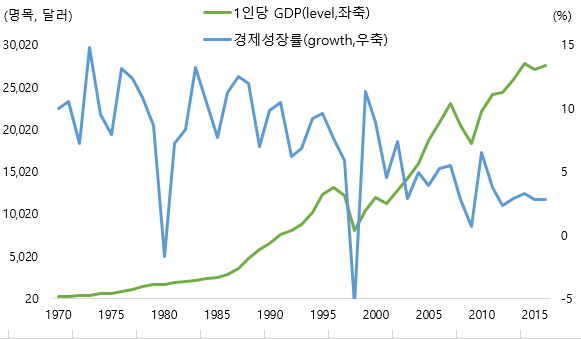
출처 : 한국은행
윗 그래프는 1970년부터 2015년까지 한국의 1인당 GDP(level) 및 경제성장률(growth) 추이를 보여주고 있습니다.
한국의 1인당 GDP는 경제발전을 시작한 이래로 줄곧 증가해 왔습니다. 1998년과 2009년에 각각 1997 동아시아 외환위기3 와 2008 글로벌 금융위기4 여파로 주춤하긴 했지만, 추세가 변하지는 않았습니다.
하지만 경제성장률은 이와 다릅니다. 과거 한국의 경제성장률은 10% 부근의 고성장을 기록해왔지만, 점차 낮아져서 현재는 2%~3% 사이에 머무르고 있습니다.
즉, '수준'(level)은 줄곧 향상되어 왔으나, '성장'(growth)은 점차 더뎌지고 있습니다.
이러한 모습은 한국에서만 관찰되는 양상이 아닙니다. 과거 미국도 높은 성장률은 기록했으나 오늘날에는 3% 부근에 머물러 있죠. 중국도 마찬가지입니다. 경제개방 이후 10%가 넘는 성장률은 기록해온 중국은 최근에는 7%~8%로 내려왔습니다.

자본량 증가에 대해 생산량 증가폭이 체감하는 모양 (diminishing)
솔로우 모형은 ''수준'(level)은 줄곧 향상되어 왔으나 '성장'(growth)은 점차 더뎌지는 모습'이 왜 나타나는지를 잘 설명해주고 있습니다.
그 이유는 '1인당 자본량 증가 → 1인당 생산량 증가'로 이어지는 경로가, 축적된 자본이 많아질수록 약해지기 때문입니다. 다르게 말해, 자본량 증가에 대한 생산량 증가폭이 체감(diminishing) 합니다.
초기 자본량이 적을 때는 자본량 한 단위가 늘어날수록 생산량도 크게 증가합니다. 삽으로 땅을 파다가 포크레인이 주어지면 작업량이 획기적으로 개선될 겁니다.
하지만 이미 가진 자본량이 많아질수록, 자본량 한 단위가 추가되어도 생산량에 별다른 변화가 없습니다. 한 사람이 포크레인 1대를 더 가진다면 번갈아가면서 사용하여 기계노후를 늦추고 생산량을 늘릴 수도 있습니다. 그런데 여기서 몇대씩 더 늘어났을때 생산량 증가 효과는 초기에 삽→포크레인으로 변했을 때의 효과보다 적어질 겁니다.
윗 그래프의 모양은 직선(linear)으로 뻗어있지 않고 구부러진 모양을 띄고 있습니다. 이것이 솔로우 모형이 상정하는 '체감하는 생산함수'(diminishing function)의 모습니다. X축 자본량이 점차 많아질수록 Y축 생산량의 증가폭은 점점 줄어듭니다.
|
이러한 논리로부터 '한 국가가 경제성장을 달성할수록(=level이 높아질수록) 성장률은 점점 하락한다(=growth 효과는 줄어든다)'는 사실을 도출해 낼 수 있습니다.
|
그리고 궁극적으로 경제성장률은 0%를 기록하게 될 겁니다. 왜 그럴까요?
자, 1인당 자본량이 계속해서 축적되어 '어느 지점'을 넘어섰다고 생각해봅시다.
저축과 투자를 통해 자본량을 더 늘리더라도 체감효과로 인해 생산량은 더 늘어나지 않습니다. 그렇다면 '자본량 증가 → 생산량 증가 → 자본량 증가'의 선순환 고리가 끊기게 되죠.
반면, 감가상각 및 인구증가율 등의 영향으로 소모되는 자본량은 일정합니다. 따라서, 1인당 자본량이 일정 지점을 넘어서면 되려 자본량이 다시 감소하는 현상이 나타납니다.
솔로우 모형은 이러한 일정 지점을 '정상상태' 혹은 '균제상태' (steady state)로 칭했습니다.
즉, 한 국가의 1인당 자본량이 '정상상태의 자본량'(steady state)보다 많이 적을수록, 그 국가는 빠르게 성장할 수 있습니다. 그리고 경제성장을 달성하면서 1인당 자본량이 정상상태에 가까워질수록 성장률이 낮아지죠. 이어서 정상상태를 초과하면 자본량이 다시 감소하여 생산량도 줄어드는 음(-)의 성장률이 나타납니다.
|
결국, 궁극적으로 그 국가의 1인당 자본량은 '정상상태'(steady state)에 머무르게 되고, 자본량은 늘지도 줄지도 않아서 성장률은 0%에서 멈추게 되고 맙니다.
|
이를 정리하면, '생활수준 향상은 얼마나 빨리 달성가능하며 언제까지 지속되는 것'인지 알 수 있습니다.
|
"경제성장을 이제 막 시작한 국가일수록 '생활수준 향상 속도가 빠르다가, 점점 늦어지며, 결국 멈추게 된다'"가 솔로우가 제시한 해답입니다.
|
※ 저축율 100%는 지속적인 성장을 이끌어낼 수 있을까?
- 저축율 증가정책은 수준효과(level effect)만 가져와
- 성장효과(growth effect) 없어, 결국 성장률은 0%로 수렴
"솔로우 모형 상에서 자본축적이 진행될수록(=1인당 자본량이 많아질수록) 성장률이 하락하여 궁극적으로 0이 된다"는 사실은 생각할꺼리를 제공해 줍니다.
한 국가의 지도자가 경제성장을 위해 경제학 공부를 하다가 솔로우 모형을 조금 알게된 상황을 떠올려 봅시다. 교과서 첫 부분만 공부하고 책을 덮은 지도자는 "저축과 투자를 늘리면 경제성장을 달성할 수 있구나. 이제 모든 국민들을 강제로 저축시켜서, 저축율 100%를 해야겠다" 라고 다짐합니다. (혹은 강력한 산아제한 정책을 통해 인구증가율 0%를 추구할 수도 있겠죠.)
하지만 솔로우 모형 뒷부분을 공부한 사람들은 이 생각이 가진 문제점을 알아챌 수 있습니다.
분명 저축율 증가 정책은 생활수준(level)의 향상을 불러올 수 있습니다. 하지만 이는 지속가능하지 않습니다. 1인당 자본량이 점점 축적될수록 성장률은 하락하여 결국 0%가 되고 맙니다.
|
따라서 우리는 지도자를 향해, "저축율 증가 정책 및 산아제한 정책은 수준효과(level effect)만 가질 뿐, 성장효과(growth effect)는 없습니다." 라고 충고 해주어야 합니다.
|
이러한 충고에 대해 "어찌됐든 생활수준이 향상됐으면 된 거 아니냐" 라고 반발할 수도 있으나, 애시당초 경제성장의 목적은 사람들의 효용과 후생을 증가시키기 위함입니다. 사람들은 소비를 통해 효용을 느끼는데, 소비를 아예 없애고 경제성장을 달성한다는 건, 경제성장의 목적이 무엇인지 모른다는 말입니다.
※ 지속적인 성장을 위한 동력은 무엇일까?
- 외생적으로 주어지는 기술진보
솔로우 모형에서 "자본량이 증가할수록 생산량 증가가 체감(diminishing)하기 때문에, 궁극적인 성장률은 0이 된다"는 사실은 매우 불행한 소리로 들립니다. 우리는 지속적인 경제성장(sustained growth)을 통해 계속해서 효용과 후생을 증대시키고 싶은데, 성장이 멈춘다는 것은 상상하기도 싫습니다.
하지만 솔로우모형에 한 가지를 추가한다면 지속적인 경제성장이 가능합니다 . 바로 '(외생적으로 주어지는) 기술진보'(exogenous technological progress) 입니다.
1인당 생산량을 늘리는 데 있어 자본축적도 중요하지만, 주어진 자본을 사람들이 얼마나 효율적으로 쓰는지도 중요합니다. 또한, 새로이 추가된 자본이 이전보다 좀 더 효율적인 형태를 띄느냐도 중요하죠. 즉, 자본축적 못지않게 '생산성'(productivity)도 중요합니다.
예를 들어, 교육수준이 높아져서 사람들의 능력이 향상 된다면 생산설비 등을 좀 더 효율적으로 사용할 수 있습니다. 또한, 이전보다 성능이 더 좋은 설비로 교체된다면 생산량이 더 많이 증가할 겁니다.
이렇게 기술수준이 점점 높아질수록 생산량을 늘려갈 수 있습니다. 생산량 증가에 있어 자본축적 이외의 또 다른 방법이 생긴 것이죠.
이때, 중요한 점은 기술진보가 생산량에 미치는 영향은 체감하지 않습니다. 자본은 한 단위 더 투입(input)해 나갈수록 생산량 증가폭이 줄어드는 체감 현상이 나타나지만, 기술진보는 그렇지 않습니다. 오히려 기술이 발전되면 될수록 생산량 증가폭은 더욱 더 커질 겁니다(increasing).
물론, 기술진보율 자체는 체감할 수 있습니다. 기술이 발전하면 할수록 한 단계 더 나은 기술을 만든다는 건 힘든 일이죠. 하지만 솔로우 모형은 기술진보율을 딱 고정시키고 전세계 어디에서나 동일하다고 가정했습니다. 그 값이 얼마이든간에, 일단 기술진보율은 '외생적으로 주어진다'고 가정했죠.
|
따라서, 1인당 자본량이 정상상태에 도달 했을지라도, 기술진보는 생산성 혁신을 불러와 1인당 생산량이 계속해서 증가하게 되고 0이 아닌 양(+)의 성장률을 기록할 수 있습니다.
|
이제 '지속적인 경제성장'이 가능하게 됐습니다. 솔로우모형 상에서 경제성장 동력(engine of growth)는 바로 '(외생적으로 주어지는) 기술진보를 통한 생산성 향상' 입니다.
※ 솔로우모형 내용 정리
자, 이번글에서 다루었던 솔로우 모형이 전달해주는 바를 한번 정리해봅시다.
● 왜 어떤 나라는 잘 살고, 또 어떤 나라는 못 사는 것일까요?
- 자본축적의 중요성
: 솔로우 모형은 이 질문에 대한 답으로 '자본축적'(Capital Accumulation)을 제시합니다. 1인당 자본을 많이 축적한 국가일수록 1인당 생산량이 많아서 부유한 국가가 됩니다.
● 자본축적 만으로 지속적인 경제성장이 가능할까?
- 불가능하다
: 자본축적 만으로는 지속적인 경제성장이 불가능 합니다. 그 이유는 자본이 한 단위 늘어났을 때 생산량 증가폭은 체감(diminishing) 하기 때문입니다.
따라서, 경제발전 초기에는 높은 성장률을 기록하다가, 경제 수준(level)이 높아질수록 성장률은 점점 하락하게 되고, 궁극적으로 0%의 성장률을 기록하게 됩니다.
● 국가별로 성장률이 각기 다른 이유는 무엇일까?
- 정상상태에서 떨어진 정도가 각기 다르다
: 2017년 오늘날 중국은 8% 대의 성장률을 기록하는 데 반해, 한국은 2%~3%에 머물러 있습니다. 그 이유는 '국가별로 정상상태(steady state)에서 떨어진 정도가 다르기 때문' 입니다.
경제성장을 시작한 지 얼마 되지 않은 중국은 아직 1인당 자본량이 정상상태에서 멀리 떨어져 있습니다. 이로 인해 높은 성장률을 기록할 수 있죠. 반면, 경제성장 성숙기에 접어든 한국은 정상상태에 가까워졌기 때문에 성장률이 낮습니다.
이를 학문용어로 표현하자면, '전이경로' 혹은 '이행기동학' (transitional dynamics) 라고 합니다. 아직 정상상태에 도달하지 못한 국가는 전이경로 속에 위치해 있습니다.
● 저축율을 높이고 인구증가율을 낮추는 정부정책이 얼마나 효과를 낼 수 있을까?
- 일시적 효과만 낼뿐, 성장효과는 없다
: 높은 저축율과 낮은 인구증가율은 1인당 자본량을 늘려서 생산량 증가를 이끌어낼 수 있습니다. 하지만 이는 일시적으로 경제수준만 높이는 효과만 낼 뿐, 결국 성장률은 0%를 기록하게 될 겁니다.
다시 말해, 이러한 정책은 수준효과(level effect)만 나타나게 할 뿐이지, 영구적인 경제성장을 위한 성장효과(growth effect)는 일으킬 수 없습니다.
● 지속적인 경제성장을 위해 필요한 동력은 무엇인가?
- 기술진보를 통한 생산성 향상
: 솔로우 모형 상에서 지속적인 경제성장을 위해 필요한 것은 인위적인 정부정책이 아니라 '(외생적으로 주어지는) 기술진보를 통한 생산성 향상' 입니다.
즉, 경제성장의 동력(engine of growth)은 '기술진보'(technological progress) 입니다.
※ 생각 뻗어나가기
▶ 자본축적 중요성이 초래하는 문제 ①
- 자본축적이 중요할까, 기술진보가 중요할까?
: 생활수준(level)을 높이기 위해서는 '자본축적'이 중요합니다. 그러나 지속적인 성장(growth)을 위해서는 '기술진보'가 필요합니다. 그렇다면 이 둘 중에 무엇이 더 중요한 것일까요?
"둘 다 중요하지. 중요성을 왜 따지냐" 라고 반문할 수 있습니다. 하지만 이는 매우 중요한 물음입니다. 만약 기술진보 없이 자본축적만 이룩한 국가는 성장률이 점점 하락하여 곧 성장이 멈추게 될 겁니다. 그러나 기술진보를 함께 진행해온 국가는 성장률을 계속 높게 유지할 수 있습니다.
우리는 '1970년대 소련 경제 · 1990년대 동아시아 경제 · 2010년대 중국 경제' 사례를 통해, '생산성 향상 없는 자본축적'이 초래하는 문제를 살펴볼 수 있습니다.
▶ 자본축적 중요성이 초래하는 문제 ②
- 미래의 경제성장을 위해서 현재의 소비를 줄여야하나?
: 경제성장(=level의 상승)을 위해서는 자본축적이 필요합니다. 자본축적은 높은 저축율을 통해 달성될 수 있습니다. 하지만 저축율이 높다는 말은 '소비가 적다'는 말과 같습니다. 그럼 "미래의 경제성장을 위해서 현재의 소비를 줄여야 할까요?"
"당연히 현재 조금 고생하고 미래에 과실을 얻어야지" 라고 생각할 수 있지만, 그리 쉬운 문제가 아닙니다.
우선, 현재의 소비 감축이 미래의 소비 증가로 이어진다는 보장이 없습니다.
만약 현재 자본축적이 전혀 이루어지지 않은 상태라면, 현재의 소비 감축(=저축 증가)은 생활수준 향상과 소득 증가를 불러와 미래의 소비를 늘릴 수 있습니다.
그러나 이미 자본축적이 많이 이루어진 상황이라면, 현재의 소비 감축(=저축 증가)은 미미한 소득 증가로 이어져서 오히려 현재+미래 소비량이 줄어들 수 있습니다.
또한, 현재의 소비 감축은 세대별로 수혜가 다릅니다. 청년 세대는 미래의 소비 증가 혜택을 누릴 수 있지만, 장년 세대는 그렇지 않습니다. 오히려 현재 소비가 줄어들어서 효용과 후생수준이 하락하는 악영향만 받습니다.
경제학자들은 현재+미래 소비량을 최대화 할 수 있는 '최적 저축율'이 얼마인지를 구하려고 노력했습니다. 이른바 '저축 수준의 황금률'(golden rule)을 찾기를 바랐죠.
그런데 우리가 이러한 고민을 하는 이유는 결국 '경제성장을 위해서는 자본축적이 필요'하기 때문입니다.
만약 솔로우 모형이 강조하는 '자본축적' 이외의 다른 방법이 있다면, 현재 고통스러운 소비 감축을 하지 않아도 됩니다.
앞으로 다른 글들을 통해 이를 살펴볼 계획입니다.
▶ 체감현상이 초래하는 문제 ①
- 모든 국가가 동일한 지점의 정상상태로 수렴할까?
: 솔로우 모형 상에서 1인당 생산량은 자본량에 대해 체감(diminishing) 하기 때문에, 결국 1인당 자본량은 정상상태(steady state)에서 멈추게 된다는 점을 살펴봤습니다.
그렇다면 모든 국가가 서로 동일한 지점의 정상상태에서 멈추는 현상이 나타날 수 있을까요?
오래전부터 경제성장을 시작해온 국가들은 이미 정상상태에 가까워졌을 겁니다. 이제 막 시작한 국가들은 정상상태를 향해 오고 있죠.
그럼 언젠가는 모든 국가가 '하나의 정상상태'에서 멈추어서 1인당 자본량 · 생산량이 모두 똑같아지는 날이 올 수도 있을겁니다.(=level이 같아짐)
게다가, 정상상태에서는 생산량이 외생적으로 주어지는 기술진보율 만큼 증가하고, 솔로우 모형은 전세계 어디에서든 기술진보율이 동일하다고 가정했습니다.
그렇다면, 언젠가는 '하나의 정상상태' 위에서, 세계 모든 국가의 성장률이 같아지는 날도 올 수 있습니다.(=growth가 같아짐)
이렇게 국가간 1인당 생산량 및 성장률이 같아지는 현상을 '수렴현상'(Convergence) 라고 부릅니다.
솔로우 모형만 살펴본다면, 전세계의 1인당 GDP가 하나로 수렴하여 국가간 격차가 없어지는 모습을 상상할 수 있습니다.
하지만 실증 데이터를 살펴보면, 솔로우 모형이 기대하는 수렴현상은 나타나지 않습니다.
빈곤국은 여전히 빈곤 상태에 머물러 있으며, 저개발 상태를 벗어난 국가들도 여전히 미국 등 선진국에 비해 낮은 수준(level)을 기록하고 있죠. 또한, 성장률 격차(growth)가 축소되는 모습은 보이지 않습니다.
그럼 솔로우 모형에 무언가 문제가 있는 것 아닐까요? 실증 결과에 반하는 이론은 아무런 의미가 없을텐데 말이죠.
앞으로 다른글을 통해, 이를 살펴볼 계획입니다.
▶ 체감현상이 초래하는 문제 ②
- 정부정책은 무용할까?
: 정부의 저축률 증가 및 인구증가율 억제 정책이 성장효과(growth effect) 없이 수준효과(level)만 내는 이유는 솔로우 모형이 '체감하는 생산함수'(diminishing function)을 가정했기 때문입니다. 꾸준한 성장을 위해서는 기술진보만 필요할 뿐입니다.
그렇다면 결국 정부정책 이라는 것은 아무런 의미가 없는 것일까요? 일부 사람들은 이를 쉽게 받아들이지 못할 겁니다. 당장 현실을 둘러봐도 정부의 법과 제도 정비, R&D 투자 지원, 교육 확대, 사회적 인프라 구축 등이 성장률을 끌어올린 모습을 볼 수 있으니까요.
그럼 우리는 '정부정책이 성장효과도 낼 수 있는 또 다른 모형'을 상상해 볼 수 있습니다.
앞으로 다른 글을 통해, 이를 살펴볼 예정입니다.
▶ 외생적인 기술진보가 초래하는 문제 ①
- 기술진보율이 모든 국가에서 같을까? 경제성장률 격차가 발생하는 이유는?
: 로버트 솔로우는 기술진보율이 모든 국가에서 동일하며 외생적으로 주어진다고 가정했습니다. 쉽게 말해, 기술진보율이 2%든 10%든 일정한 값으로 모든 국가에 나타난다는 것이죠.
그런데 기술진보율이 모든 국가에서 같을 수 있을까요?
당장 미국과 한국을 대비해봐도, 양국간의 기술진보율에 차이가 있다는 점을 인식할 수 있습니다. 미국은 혁신을 통해 끊임없이 새로운 기술을 창출하고 실제 기업운영에 도입하고 있습니다. 한국 또한 기술진보를 이루어내고 있지만, 미국에 비해서 뒤쳐진다는 점을 부인할 수 없습니다.
"기술진보율이 모든 국가에서 동일하다"는 가정이 성립하는 이유는 '기술은 공공재(public goods)' 라고 생각하기 때문입니다.
공공재란 비배제성(non-excludable) · 비경합성(non-rivalry) 을 띄는 재화로서, '모든' 사람들이 '동시에' 사용할 수 있습니다. 따라서, 공공재는 여러 사람에게 빠르게 확산(diffusion)되는 특징을 지니고 있습니다.
그러나 실제 기술은 공공재 특성을 띄고 있지 않습니다. 많은 기술은 '특허제도'(patent)를 통해 보호되고 있으며(=배제성을 띄고 있으며), 다른 국가에 유출될 가능성을 엄격히 차단하고 있습니다.
즉, 기술은 공공재가 아니며, 기술진보율은 국가별로 서로 다를 수 있습니다.
만약 기술진보율이 국가별로 다르다면, 경제성장률 격차가 발생하는 이유도 다르게 볼 수 있습니다.
솔로우 모형은 성장률 격차의 원인을 '전이경로'(transitional dynamics)로 보고 있습니다. 국가별로 정상상태에서 떨어진 정도가 다르다는 점을 강조하죠.
하지만 기술진보율이 다르다면, '기술격차'(technology gap)가 성장률 격차의 원인이 될 수 있습니다. 새로운 기술을 빨리 전달받지 못하는 폐쇄형 국가일수록 혹은 기술을 이용할 잠재력이 떨어지는 국가일수록 성장률이 뒤떨어지기 때문입니다.
"기술격차가 존재하는가 · 기술은 공공재인가 · 기술 확산은 어떻게 일어나는가"는 경제성장론 발전 과정에서 큰 역할을 한 쟁점입니다.
앞으로 다른글을 통해, 이러한 쟁점이 경제성장론 역사(?)에서 어떠한 역할을 했는지 살펴볼 겁니다.
▶ 외생적인 기술진보가 초래하는 문제 ②
- 왜 기술진보가 '외생적'으로 발생하나?
: '외생적인 기술진보'를 둘러싸고 던질 수 있는 또 다른 물음은 "왜 기술진보가 '외생적'으로 주어지는가?" 입니다.
기술진보는 하늘에서 떡하니 떨어지는 게 아닙니다. 기업이 R&D에 얼마나 투자하느냐 / 과학자 및 공학자들이 얼마나 힘을 쓰느냐 / 국가의 R&D 지원 정책이 얼마인가 / 다른 국가로부터 진보된 기술을 얼마나 빨리 받아들이냐 등등 여러 경제주체들의 행위가 결합된 결과물 입니다.
다르게 말해, 현실에서 기술진보는 '내생적'(endogenous)으로 결정됩니다. 그런데 솔로우 모형은 기술진보를 '외생적'(exogenous)으로 간주했습니다.
교과서 [경제성장론] 3편 - 자본에 대한 이해 (솔로우 모형)
저번 시간에는, 경제학에서 가장 중요한 생산투입요소는 자본과 노동이며, 이들의 투입량을 증대시키면 생산량 또한 증가한다는 것을 배웠습니다. 오늘은 이들 중, 자본에 대해서 자세하게 알
alittlecane.tistory.com
저번 시간에는, 경제학에서 가장 중요한 생산투입요소는 자본과 노동이며, 이들의 투입량을 증대시키면 생산량 또한 증가한다는 것을 배웠습니다. 오늘은 이들 중, 자본에 대해서 자세하게 알아 보겠습니다.
우리는 왜 자본을 '투자'할까요? 알기 쉽게 자본을 돈이라는 단어로 바꿔 생각해 봅시다. 돈은 쓰기 위해 법니다. 하지만 우리는 번 돈의 전부를 쓰지 않습니다. 그 중에 일부는 저축을 하는데 사용합니다.
왜 저축을 할까요? 왜냐하면 오늘 저축한 1원의 돈은 훗날 그 돈을 찾을 때 1원 이상이 되어 있기 때문입니다.
즉, 우리는 미래에 더 큰 돈을 얻기 위해 오늘 번 돈을 오늘 다 써 버리지 않고, 그 중 일부를 저축하거나 투자합니다. 지금 제가 저축이란 용어와 투자라는 용어를 혼용하여 쓰고 있는데, 그 이유는 사실상 이 두 가지가 같은 것이기 때문입니다. 왜 오늘 저축한 1원은 미래에 1원 이상이 될까요?
왜냐하면, 우리가 저축한 돈을 가지고 은행이 우리를 대신하여 다른 누군가에게 투자했기 때문입니다. 누군가가 그 돈을 사용하여 생산활동을 하고, 그 생산활동을 통해 수익을 발생시켰기에, 그 수익의 일부를 여러분도 이자라는 형태로 나눠 갖게 되는 것입니다.
즉, 투자란, 생산활동을 통해 발생한 소득을 그 해에 전부 소비해 버리는 것이 아니라, 미래에 더 큰 소득을 발생시킬 것을 기대하고 다시 생산활동에 투입하는 것을 말합니다. 즉, 농부가 곡식을 추수하여 모두 먹어버리지 않고, 일부를 다음 해에 뿌릴 씨앗으로 남겨 놓았다면, 이것이 투자인 것입니다.
즉, 오늘의 투자는 내일의 생산량을 증대시킵니다. 버는 족족 소비하여 버리고, 내일을 위해 투자하지 않는 나라의 경제는 성장할 수 없습니다.
이쯤에서 거시경제학을 공부할 때 안 보고 지나칠 수 없는, '솔로우 모형'을 간략히 설명하도록 하겠습니다. 솔로우 모형은 그래프와 수식으로 우리의 기를 죽이지만, 사실 앞서 제가 말한 것들을 다른 방식으로 표현한 것에 지나지 않습니다. 아래의 그래프를 보시죠.
위 그래프에서 가로축은 현재의 자본량입니다. 왼쪽에서 오른쪽으로 갈수록 그 국가는 더 많은 자본을 보유하고 있습니다. 보통 못 사는 나라는 가로축의 왼쪽 부분에, 잘 사는 나라는 가로축의 오른쪽 부분에 위치하고 있겠지요.
현재 A라는 국가의 자본량이 가로축의 왼쪽 부근에 위치해 있다고 합시다. 가로축상 A국가의 위치에서 세로로 가상의 선을 쭉 그어 보면 그 가상의 선이 세가지 색깔의 그래프와 각각 만납니다. 그리고 위에서부터 보았을 때, 파란색의 그래프가 가상의 선과 가장 먼저 만나는 것을 볼 수 있으실 것입니다.
가상의 선과 파란색 그래프가 만난 지점, 그 지점의 높이만큼 그 국가는 재화를 산출합니다. 그리고 다음으로 만나는 그래프가 빨간색 그래프라는 것을 보실 수 있습니다.
가상의 선과 빨간색 그래프가 만난 지점, 그 지점의 높이만큼 그 국가는 다음 해를 위해 투자합니다.
다시 말하자면, A라는 국가는 파란색 높이만큼을 벌어서, 파란색 그래프와 빨간색 그래프 사이의 공간만큼만을 소비한 후, 빨간색 그래프 높이만큼은 미래를 위해 투자합니다.
그렇다면 이렇게 투자된 자본은 전부 미래를 위해 사용될까요? 그렇지 않습니다. 우리는 여기서, 검은색 그래프가 의미하는 '감가상각'이 무엇인지 이해하고 넘어가야 합니다. 감가상각이란 쉽게 말해서 매 해 사라져 버리는 자본을 말합니다. 바람이 쓸려 바위가 깎이듯이 매 해 슬금슬금 자본이 소멸해 버리는 것입니다.
예를 들어, 여러분이 공장을 가지고 있다고 합시다. 처음에는 최신식 기계를 들여 놓겠지만, 시간이 가면서 점차 고장도 나고, 녹도 슬고, 기능을 잃어가겠지요? 그러다가 어느 순간이 되면 아예 기계가 멈춰 버려 새 것으로 재 구매를 해야할 때도 올 것입니다. 이것이 바로 자본의 자연적 성격인 '감가상각'입니다.
따라서, 여러분이 투입하는 자본의 일부는, 감가상각된 자본을 보전하는 데에 사용됩니다. 이것이 무슨 말이냐구요? 방금 감가상각이란, 시간이 지날 수록 기계가 고장이 나는 것이다고 했습니다.
고장난 것은 일단 고치고 봐야 겠지요? 예를 들어 볼까요? 여러분이 공장을 돌려서 300만원을 벌었습니다. 여러분은 그 중 200만원 어치만 생활비로 쓰고, 나머지 100만원은 새로운 기계를 사는데 쓰기로 결심했습니다.
그런데, 100만원을 들고 공장에 딱 가봤더니 이미 가지고 있는 기계가 고장이 나서 20만원의 수리비가 나가게 된 것입니다. 그렇다면, 여러분이 100만원을 그 해에 투자하기로 결심했다고 해도, 실제로 새로운 기계를 사는데 쓸 수 있는 돈은, 감가상각비 20만원을 제하고 남은 80만원 어치가 될 것입니다.
그것이 위 그래프에서 검은색 그래프가 말하고 있는 부분입니다. 즉, 여러분이 빨간색 그래프 높이만큼 다음 해의 생산활동에 투자하기로 결심했다고 해도, 검은색 그래프의 높이만큼은 감가상각이라는 이름으로 저절로 깎여 나가기에, 실제로 여러분이 다음 해에 투자할 수 있는 자본의 양은 빨간색 그래프와 검은색 그래프 사이의 차이만큼만이 되는 것입니다.
자, 그래도 빨간색 그래프와 검은색 그래프 사이의 차이만큼은 남았습니다. 이제 다음은 어떻게 될까요? 처음 이야기를 시작할 때, 가로축은 한 국가의 현재 자본량을 말한다고 했지요? 그런데 현재 그 국가가, 빨간색 그래프와 검은색 그래프 사이의 차이만큼의 자본을 다음 해를 위해 투자하였습니다.
그렇다면 다음 해에는, 그 국가의 총 자본량이, 현재의 자본량에 더하여 새로 투입한 자본량만큼 증가하겠지요? 따라서, 다음 해의 그 국가의 총 자본량의 위치는 가로축 상에서, 현재 위치한 부분보다 오른쪽으로 좀 더 이동할 것입니다.
그 부분에서 다시 가상의 선을 그어 보면, 저번에 위치했던 곳보다 산출량도 더 많고, 그에 따른 투자량도 더 증대되어 있음을 볼 수 있을 것입니다. 이상의 내용을 그림으로 다시 보여 드리면 다음과 같습니다.
그렇다면, 언제까지 이러한 과정은 지속 될까요? 경제학에서 배우는 중요한 개념으로 '한계생산 체감의 법칙'이라는 것이 있습니다. 쉽게 생각하면 생산량의 증대에는 한계가 있다는 것입니다. 도깨비 방망이처럼 경제가 무한히 같은 속도로 성장하면 얼마나 좋겠습니까만은, 때가 되면 성장률은 줄어들기 마련입니다.
경제규모가 100인 나라가 110이 되는 것과, 경제규모가 10,000인 나라가 11,000이 되는 것을 비교하면, 같은 10%의 성장이라고 해도 전자가 훨씬 쉽겠지요. 따라서, 경제규모의 성장에 따라, 절대적 성장은 계속될 지 몰라도, 경제 성장률 자체는 점차 줄어들게 됩니다.
처음에 투자에 대해 이야기할 때, 투자란 전체 생산한 것 중에 미래 생산 증대를 목적으로 다음 해의 생산활동에 재투입되는 것들이다고 했지요?
따라서, 투자율은 전체 생산량에 대한 비율로 나타내어 집니다. 그런데 앞서서 '한계생산 체감의 법칙'이라는 것 때문에 경제 규모가 커질 수록 경제 성장률 또한 점차 줄어든다고 했지요? 따라서, 이에 비례하는 투자의 증가량도 점차 줄어들게 됩니다.
이것이 바로, 앞서 보여드린 솔로우 모형의 그래프에서 산출량을 나타내는 파란색 그래프와 투자량을 나타내는 빨간색의 그래프가 직선으로 뻗어 나가지 않고 자본 규모가 커지면 커질 수록 아래로 처지는 이유입니다.
그런데, 감가상각을 나타내는 검은색 그래프는 그 증가하는 양이 줄어들지 않습니다. 왜 일까요? 앞서서, 감가상각이란 기계 고장으로 인한 수리비라고 했습니다.
그렇다면 기계가 많으면 많을수록 수리비도 더 들겠지요? 만약 100만원 어치의 기계가 있을 때 20만원의 수리비가 들었다고 하면, 200만원 어치의 기계가 있다면, 40만원이 들 것입니다.
즉 솔로우 모형은, 기계가 늘어나면 수리비도 똑같이 늘어나지, 그 늘어나는 속도가 줄거나 늘지 않는다고 보고 있습니다. 기계가 2배가 되면, 수리비도 2배가 되는 것입니다.
투자의 증가율은 점차 줄어드는데, 감가상각의 증가율은 일정하다... 그렇다면 이 둘이 만나는 날이 오겠지요? 위 그래프에서 빨간색 그래프와 검은색 그래프가 결국 교차하듯이 말입니다.
예를 들어 말하자면, 새로 기계를 사기 위해 마련하는 돈은 110만원, 115만원, 118만원, ...처럼 늘어나는 속도가 점차 줄어드는데, 수리비는 30만원, 40만원, 50만원, ...처럼 지속적으로 증가하는 것입니다. 그러다보면 어느 순간, 기계를 사기 위해 마련한 돈도 150만원, 수리비도 150만원인 순간이 올 것입니다.
이 때가 되면, 매년 신규투자비용으로 150만원을 마련하여도, 그 돈 전부가 기존 기계를 '유지'하는데에 쓰이고, 실제로 다음 해를 위해 사들이는 기계는 없는 상태가 계속 이어지게 됩니다. 이 때가 되면, 새로 사들이는 기계가 없기 때문에 감가상각비용도 더 이상 증가하지 않습니다. 또한, 실제로 더 사들이는 기계가 없기 때문에 경제수준도 더 이상 성장하지 않고 그 자리에 머물게 됩니다.
이 지점이 위 그래프에 표시된 K* 지점입니다. 이 지점에서 경제는 안정상태로 들어서게 되고, 성장을 멈추게 됩니다.
그러나 솔로우 모형이 말하고자 하는 중요한 사실은, 경제의 성장이 언젠가 멈춘다는 것이 아닙니다. 더 중요한 사실은, 가로축에서 K* 의 좌측에 위치한 모든 국가들은 K* 에 이를 때까지 경제성장의 레이스를 지속한다는 사실입니다. 또한, 수정된 솔로우 모형에서는 K* 또한 지속적으로 우측으로 이동할 수 있기 때문에, 사실상 투자만 지속된다면 모든 국가들은 오른쪽을 향한 레이스를 계속할 수 있는 것이지요.
지금까지 배운 내용을 정리하면 다음과 같습니다.
'국가는 그 해 생산한 것들 중 일부를 다음 해 생산을 증대시키기 위해 생산활동에 다시 투입할 수 있고, 이것을 우리는 투자라 부른다.
투자된 자본 중 그 해 감가상각을 cover하고 남은 자본만큼이 다음 해에 실제로 투자된다. 자본이 새로 투입되었기에 다음 해의 생산량도 증가한다.
생산이 증대된 만큼 그 국가는 더 많은 자본을 다다음 해를 위해 투자할 수 있지만, 점차 생산과 투자의 증가량은 감소하는 반면 감가상각의 증가량은 일정하기 때문에
어느 순간이 되면 전체 투자가 매 해 그 해의 감가상각만 보전하는 상태에 이르게 되고 경제 성장은 종료된다.'
이제 결론입니다. 그렇다면, 어떻게 하면 경제를 더 빠르게 성장시킬 수 있을까요? 새로 투입되는 자본만큼 경제도 성장한다고 하였으니, 새로 투입되는 자본의 양을 더 늘리면 되겠지요. 그래프에서 보자면, 빨간색 그래프와 검은색 그래프의 차이만큼 오른쪽으로 이동한다고 했으니, 빨간색 그래프를 위로 이동시켜 그 차이를 증대시키면 될 것입니다. 그런데 빨간색 그래프는 투자양을 나타내므로, 빨간색 그래프를 위로 이동시킨다는 것은 전체 산출량에서 다음 해 생산을 위해 투자되는 비율, 즉 투자율을 증대시킨다는 말과 같은 것이지요.
즉, 오늘 배운 것을 한줄로 요약하자면, '경제 성장의 속도를 증대하고 싶다면, 투자율을 늘려라' 정도가 되겠네요. 결국 경제학이라는 것이, 상식의 검증이라는 생각이 들지요?
다음 편에서는 또 하나의 중요한 생산투입요소인 '노동'에 대해 알아 보겠습니다.
- 3편 끝 (이상의 내용은 David N. Weil 교수님의 'Economic Growth' 을 바탕으로 작성하였습니다.)
